Portal:Mathematics

The Mathematics Portal

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

Featured articles are displayed here, which represent some of the best content on English Wikipedia.

$Image 1 Portrait by August Köhler, c. 1910, after 1620 original Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium. Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)$

Image 1

Portrait by August Köhler, c. 1910, after 1620 original

Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 2

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kih-MEE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and analysis by applying the concept of the infinitesimals and the method of exhaustion to derive and rigorously prove many geometrical theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also said to have built a planetarium device that demonstrated the movements of the known celestial bodies, and may have been a precursor to the Antikythera mechanism. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 3
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 4

The title page of a 1634 version of Hues's Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.

In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues's work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
Image 5

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter $\pi$ (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation $f(x)$ for the value of a function, the letter $i$ to express the imaginary unit ${\sqrt {-1}}$ , the Greek letter $\Sigma$ (capital sigma) to express summations, the Greek letter $\Delta$ (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant $e$ , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
Image 6

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 7

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in 17th-century studies of probability and annuities. Actuaries in the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems; actuaries use this knowledge to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
Image 8
The number π (/paɪ/ ; spelled out as pi) is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 9

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 10
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with an operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition operation form a group.

The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. (Full article...)
Image 11

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. A mathematics prodigy, he abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle and lone wolf terrorism campaign.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored a roughly 35,000-word manifesto and social critique called Industrial Society and Its Future which opposes all forms of technology, rejects leftism and fascism, advocates cultural primitivism, and ultimately suggests violent revolution. (Full article...)
Image 12

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 13
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
Image 14

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.

Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
Image 15
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

Thus the hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

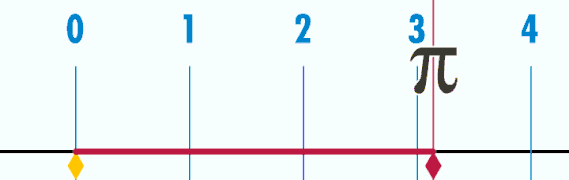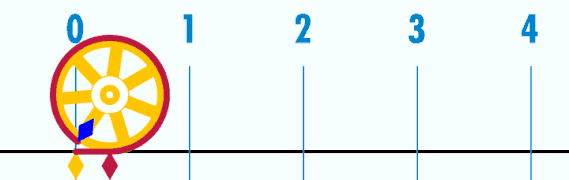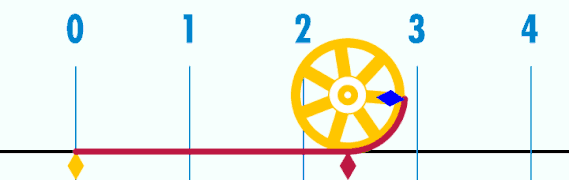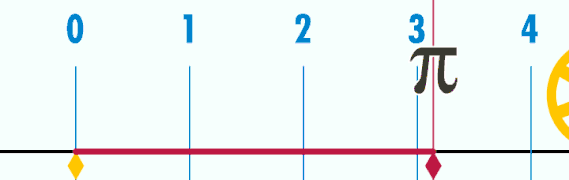
Selected image –

animation of the act of "unrolling" a circle's circumference, illustrating the ratio pi (π)

Pi

Credit: John Reid

Pi, represented by the Greek letter π, is a mathematical constant whose value is the ratio of any circle's circumference to its diameter in Euclidean space (i.e., on a flat plane); it is also the ratio of a circle's area to the square of its radius. (These facts are reflected in the familiar formulas from geometry,

C = π d

and

A = π r 2

.) In this animation, the circle has a diameter of 1 unit, giving it a circumference of π. The rolling shows that the distance a point on the circle moves linearly in one complete revolution is equal to π. Pi is an irrational number and so cannot be expressed as the ratio of two integers; as a result, the decimal expansion of π is nonterminating and nonrepeating. To 50 decimal places, π ≈ 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510, a value of sufficient precision to allow the calculation of the volume of a sphere the size of the orbit of Neptune around the Sun (assuming an exact value for this radius) to within 1 cubic angstrom. According to the Lindemann–Weierstrass theorem, first proved in 1882, π is also a transcendental (or non-algebraic) number, meaning it is not the root of any non-zero polynomial with rational coefficients. (This implies that it cannot be expressed using any closed-form algebraic expression—and also that solving the ancient problem of squaring the circle using a compass and straightedge construction is impossible). Perhaps the simplest non-algebraic closed-form expression for π is

4 arctan 1

, based on the inverse tangent function (a transcendental function). There are also many infinite series and some infinite products that converge to π or to a simple function of it, like 2/π; one of these is the infinite series representation of the inverse-tangent expression just mentioned. Such iterative approaches to approximating π first appeared in 15th-century India and were later rediscovered (perhaps not independently) in 17th- and 18th-century Europe (along with several continued fractions representations). Although these methods often suffer from an impractically slow convergence rate, one modern infinite series that converges to 1/π very quickly is given by the Chudnovsky algorithm, first published in 1989; each term of this series gives an astonishing 14 additional decimal places of accuracy. In addition to geometry and trigonometry, π appears in many other areas of mathematics, including number theory, calculus, and probability.

Good articles –

These are Good articles, which meet a core set of high editorial standards.

Image 1
Graph of $log 2 x$ as a function of a positive real number $x$

In mathematics, the binary logarithm ( $log 2 n$ ) is the power to which the number $2$ must be raised to obtain the value $n$ . That is, for any real number $x$ ,
: $x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.$
For example, the binary logarithm of $1$ is $0$ , the binary logarithm of $2$ is $1$ , the binary logarithm of $4$ is $2$ , and the binary logarithm of $32$ is $5$ .

The binary logarithm is the logarithm to the base $2$ and is the inverse function of the power of two function. There are several alternatives to the $log 2$ notation for the binary logarithm; see the Notation section below. (Full article...)
Image 2

Walker c. 1885

Francis Amasa Walker (July 2, 1840 – January 5, 1897) was an American economist, statistician, journalist, educator, academic administrator, and an officer in the Union Army. As a prolific author and the third president of the Massachusetts Institute of Technology (MIT) until his death in 1897, Walker was a leading political economist and advocate for a policy of bimetallism by international agreement. His scholarly contributions are widely recognized as having broadened, liberalized, and modernized economic and statistical theory with contributions to wages, wealth distribution, money, and social economics, and he is credited with developing the residual theory of wage distribution.

Walker was born into a prominent Boston family, the son of the economist and politician Amasa Walker, and he graduated from Amherst College at the age of 20. He received a commission to join the 15th Massachusetts Infantry and quickly rose through the ranks as an assistant adjutant general. Walker fought in the Peninsula, Bristoe, Overland, and Richmond-Petersburg Campaigns before being captured by Confederate forces and held at the infamous Libby Prison. In July 1866, he was awarded the honorary grade of brevet brigadier general United States Volunteers, to rank from March 13, 1865, when he was 24 years old. (Full article...)
Image 3

Wigner in 1963

Eugene Paul Wigner (Hungarian: Wigner Jenő Pál, pronounced [ˈviɡnɛr ˈjɛnøː ˈpaːl]; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles".

A graduate of the Technical Hochschule Berlin (now Technische Universität Berlin), Wigner worked as an assistant to Karl Weissenberg and Richard Becker at the Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone in the mathematical formulation of quantum mechanics. He is also known for his research into the structure of the atomic nucleus. In 1930, Princeton University recruited Wigner, along with John von Neumann, and he moved to the United States, where he obtained citizenship in 1937. (Full article...)
Image 4
A polyhedron and its midsphere. The red circles are the boundaries of spherical caps within which the surface of the sphere can be seen from each vertex.

In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals (Catalan solids) all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere.

When a polyhedron has a midsphere, one can form two perpendicular circle packings on the midsphere, one corresponding to the adjacencies between vertices of the polyhedron, and the other corresponding in the same way to its polar polyhedron, which has the same midsphere. The length of each polyhedron edge is the sum of the distances from its two endpoints to their corresponding circles in this circle packing. (Full article...)
Image 5
Kissing circles. Given three mutually tangent circles (black), there are, in general, two possible answers (red) as to what radius a fourth tangent circle can have.

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

Frederick Soddy's 1936 poem The Kiss Precise summarizes the theorem in terms of the bends (signed inverse radii) of the four circles: (Full article...)
Image 6

Equilateral form of the Cairo tiling

In geometry, a Cairo pentagonal tiling is a tessellation of the Euclidean plane by congruent convex pentagons, formed by overlaying two tessellations of the plane by hexagons and named for its use as a paving design in Cairo. It is also called MacMahon's net after Percy Alexander MacMahon, who depicted it in his 1921 publication New Mathematical Pastimes. John Horton Conway called it a 4-fold pentille.

Infinitely many different pentagons can form this pattern, belonging to two of the 15 families of convex pentagons that can tile the plane. Their tilings have varying symmetries; all are face-symmetric. One particular form of the tiling, dual to the snub square tiling, has tiles with the minimum possible perimeter among all pentagonal tilings. Another, overlaying two flattened tilings by regular hexagons, is the form used in Cairo and has the property that every edge is collinear with infinitely many other edges. (Full article...)
Image 7
Modus ponens is one of the main rules of inference.

Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the logical structure of valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. Modus ponens, an influential rule of inference, connects two premises of the form "if $P$ then $Q$ " and " $P$ " to the conclusion " $Q$ ", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as modus tollens, disjunctive syllogism, constructive dilemma, and existential generalization.

Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallacies—invalid argument forms involving logical errors. (Full article...)
Image 8
A Doyle spiral of type (8,16) printed in 1911 in Popular Science as an illustration of phyllotaxis. One of its spiral arms is shaded.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.

Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or early 1990s. However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early 1900s. (Full article...)
Image 9
Lighting and reflection calculations, as in the video game OpenArena, use the fast inverse square root code to compute angles of incidence and reflection.

Fast inverse square root, sometimes referred to as Fast InvSqrt() or by the hexadecimal constant 0x5F3759DF, is an algorithm that estimates ${\textstyle {\frac {1}{\sqrt {x}}}}$ , the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number $x$ in IEEE 754 floating-point format. The algorithm is best known for its implementation in 1999 in Quake III Arena, a first-person shooter video game heavily based on 3D graphics. With subsequent hardware advancements, especially the x86 SSE instruction rsqrtss, this algorithm is not generally the best choice for modern computers, though it remains an interesting historical example.

The algorithm accepts a 32-bit floating-point number as the input and stores a halved value for later use. Then, treating the bits representing the floating-point number as a 32-bit integer, a logical shift right by one bit is performed and the result subtracted from the number 0x5F3759DF, which is a floating-point representation of an approximation of ${\textstyle {\sqrt {2^{127}}}}$ . This results in the first approximation of the inverse square root of the input. Treating the bits again as a floating-point number, it runs one iteration of Newton's method, yielding a more precise approximation. (Full article...)
Image 10

Portrait of Newton, 1689

Sir Isaac Newton (4 January [O.S. 25 December] 1643 – 31 March [O.S. 20 March] 1727) was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Enlightenment that followed. His book Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687, achieved the first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science.

In the Principia, Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. He used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for tides, the trajectories of comets, the precession of the equinoxes and other phenomena, eradicating doubt about the Solar System's heliocentricity. Newton solved the two-body problem, and introduced the three-body problem. He demonstrated that the motion of objects on Earth and celestial bodies could be accounted for by the same principles. Newton's inference that the Earth is an oblate spheroid was later confirmed by the geodetic measurements of Alexis Clairaut, Charles Marie de La Condamine, and others, convincing most European scientists of the superiority of Newtonian mechanics over earlier systems. He was also the first to calculate the age of Earth by experiment, and described a precursor to the modern wind tunnel. (Full article...)
Image 11
Mathematics in art: Albrecht Dürer's copper plate engraving Melencolia I, 1514. Mathematical references include a compass for geometry, a magic square and a truncated rhombohedron, while measurement is indicated by the scales and hourglass.

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

Mathematics and art have a long historical relationship. Artists have used mathematics since the 4th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions conjectured to have been based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient art and architecture, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De divina proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of the golden ratio in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesburg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim. In Islamic art, symmetries are evident in forms as varied as Persian girih and Moroccan zellige tilework, Mughal jali pierced stone screens, and widespread muqarnas vaulting. (Full article...)
Image 12
In mathematics, economics, and computer science, the Gale–Shapley algorithm (also known as the deferred acceptance algorithm, propose-and-reject algorithm, or Boston Pool algorithm) is an algorithm for finding a solution to the stable matching problem. It is named for David Gale and Lloyd Shapley, who published it in 1962, although it had been used for the National Resident Matching Program since the early 1950s. Shapley and Alvin E. Roth (who pointed out its prior application) won the 2012 Nobel Prize in Economics for work including this algorithm.

The stable matching problem seeks to pair up equal numbers of participants of two types, using preferences from each participant. The pairing must be stable: no pair of matched participants should mutually prefer each other to their assigned match. In each round of the Gale–Shapley algorithm, unmatched participants of one type propose a match to the next participant on their preference list. Each proposal is accepted if its recipient prefers it to their current match. The resulting procedure is a truthful mechanism from the point of view of the proposing participants, who receive their most-preferred pairing consistent with stability. In contrast, the recipients of proposals receive their least-preferred pairing. The algorithm can be implemented to run in time quadratic in the number of participants, and linear in the size of the input to the algorithm. (Full article...)

Did you know (auto-generated) –

... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
... that Leonardo da Vinci invented a device to solve Alhazen's problem, instead of finding a mathematical solution?
... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that Ewa Ligocka cooked another mathematician's goose?
... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?

More did you know –

Did you know...

... that one can list every positive rational number without repetition by breadth-first traversal of the Calkin–Wilf tree?
... that the Hadwiger conjecture implies that the external surface of any three-dimensional convex body can be illuminated by only eight light sources, but the best proven bound is that 16 lights are sufficient?
... that an equitable coloring of a graph, in which the numbers of vertices of each color are as nearly equal as possible, may require far more colors than a graph coloring without this constraint?
... that no matter how biased a coin one uses, flipping a coin to determine whether each edge is present or absent in a countably infinite graph will always produce the same graph, the Rado graph?
...that it is possible to stack identical dominoes off the edge of a table to create an arbitrarily large overhang?
...that in Floyd's algorithm for cycle detection, the tortoise and hare move at very different speeds, but always finish at the same spot?
...that in graph theory, a pseudoforest can contain trees and pseudotrees, but cannot contain any butterflies, diamonds, handcuffs, or bicycles?

Selected article –

Problem II.8 in the Arithmetica by Diophantus, annotated with Fermat's comment, which became Fermat's Last Theorem
Image credit:

Fermat's Last Theorem is one of the most famous theorems in the history of mathematics. It states that:

a^{n}+b^{n}=c^{n}

has no solutions in non-zero integers

a

,

b

, and

c

when

n

is an integer greater than 2.

Despite how closely the problem is related to the Pythagorean theorem, which has infinite solutions and hundreds of proofs, Fermat's subtle variation is much more difficult to prove. Still, the problem itself is easily understood even by schoolchildren, making it all the more frustrating and generating perhaps more incorrect proofs than any other problem in the history of mathematics.

The 17th-century mathematician Pierre de Fermat wrote in 1637 in his copy of Bachet's translation of the famous Arithmetica of Diophantus: "I have a truly marvelous proof of this proposition which this margin is too narrow to contain." However, no correct proof was found for 357 years, until it was finally proven using very deep methods by Andrew Wiles in 1995 (after a failed attempt a year before). (Full article...)

View all selected articles

Subcategories

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Applied mathematics

Mathematicians

Women in mathematics

Works about mathematics

Mathematics-related lists

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Applied mathematics

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z