List of polyhedral stellations

In three-dimensional space, a stellation extends facets of a polyhedron to form a new figure. Usually, this is achieved by extending faces or edges and planes of a polyhedron, until they generate new vertices that bound a newly formed figure.

This article mainly lists various stellations belonging to uniform polyhedra, such as those of the regular Platonic solids and the semiregular Archimidean solids. It also lists stellations featuring unbounded vertices.

Background

Star polytopes

Further information: Kepler–Poinsot polyhedron § History
Model of the final stellation of the icosahedron by Max Brückner, as part of his 1900 book, Vielecke und Vielflache: Theorie und Geschichte[1]

Experimentation with star polygons and star polyhedra since the fourteenth century AD led the way to formal theories for stellating polyhedra:

It was in 1619 that the first mathematical description of a stellation was given, by Johannes Kepler in his landmark book, Harmonice Mundi: the process of extending the edges (or faces) of a figure until they meet again to obtain a new figure. Using this method, Kepler was able to discover the small stellated dodecahedron and the great stellated dodecahedron. In 1809, Louis Poinsot rediscovered Kepler's figures by putting together star pentagons around each vertex. He also assembled convex polygons around star vertices, leading him to discover two more regular stars, the great icosahedron and great dodecahedron. Three years later, Augustin-Louis Cauchy proved, using concepts of symmetry, that these four stellations are the only regular star-polyhedra, eventually termed the Kepler–Poinsot polyhedra.

Stellation process

Further information: Stellation § Stellating polyhedra

Coxeter et al. (1938) details, for the first time, stellations of the regular icosahedron with specific rules proposed by J. C. P. Miller.[8] Generalizing these (Miller's rules) for stellating any uniform polyhedron yields the following:[9]

  • The faces must lie in face-planes, i.e., the bounding planes of the regular solid.
  • All parts composing the faces must be the same in each plane, although they may be quite disconnected.
  • The parts included in any one plane must be symmetric about corresponding point groups, without or with reflection. This secures polyhedral symmetry for the whole solid.
  • All parts included in planes must be "accessible" in the completed solid (i.e. they must be on the "outside").
  • Cases where the parts can be divided into two sets, each giving a solid with as much symmetry as the whole figure, are excluded from consideration; combination of enantiomorphous pairs having no common part (which actually occurs in just one case) are included.

These rules are ideal for stellating smaller uniform solids, such as the regular polyhedra; however, when assessing stellations of other larger uniform polyhedra, this method can quickly become overwhelming. (For example, there are a total of 358,833,072 stellations to the rhombic triacontahedron using this set of rules.)[10] To address this, Pawley (1973) proposed a set of rules that restrict the number of stellations to a more manageable set of fully supported stellations that are radially convex,[11][12] such that an outward ray from the center of the original polyhedron (in any direction) crosses the stellation surface only once[9] (that is to say, all visible parts of a face are seen from the same side).

H. S. M. Coxeter was the first to describe the stellation process as the reciprocal action to faceting, in his 1948 first edition of Regular Polytopes.[13] He further specifies the construction of a star polyhedron as a stellation of its core (with congruent face-planes), or by faceting its case — the former requires the addition of solid pieces that generate new vertices, while the latter involves the removal of solid pieces, without forming any new vertices.[14][b]

Lists

Lists for polyhedral stellations contain non-convex polyhedra; some of the most notable examples include:[c]

Examples of stellations that topologically do not fit into standard definitions of uniform polyhedra are listed further down (i.e. stellations of hemipolyhedra).[16]

Stellations of various polyhedra
Image Name Stellation core Ref. Notes
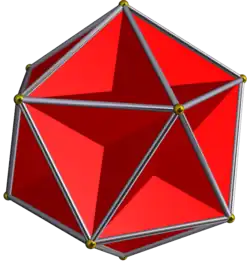Great dodecahedron Regular dodecahedron
W21
*, ¶
Great stellated dodecahedron
W22
Small stellated dodecahedron
W20
*
Great icosahedron Regular icosahedron
W41,C7
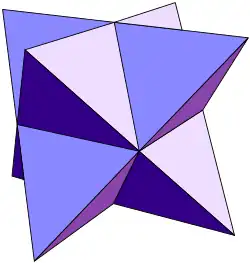Stellated octahedron Regular octahedron
W19
†, ‡, ¶
Compound of five tetrahedra Regular icosahedron
W24,C47
†
Compound of five octahedra
W2,C3
Compound of ten tetrahedra
W25,C22
Compound of five cubes Rhombic triacontahedron
[17]
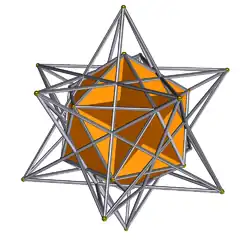Compound of great dodecahedron and small stellated dodecahedron
[18]
‡
Compound of dodecahedron and icosahedron Icosidodecahedron
W47
Compound of great icosahedron and great stellated dodecahedron
W61
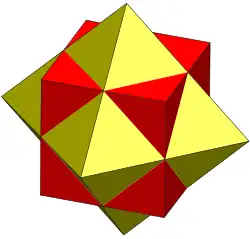Compound of cube and octahedron Cuboctahedron
W43
Small triambic icosahedron Regular icosahedron
W1,C2
Final stellation of the icosahedron
W13,C8
First stellation of the rhombic dodecahedron Rhombic dodecahedron
[19]
[d]
KEY

* Kepler-Poinsot polyhedron
† Regular compound polyhedron
‡ Platonic or Kepler-Poinsot dual polyhedra
First and/or outermost stellation

"Ref." (references) such as indexes found in Coxeter et al. (1999) using the Crennells' illustration notation (C), and Wenninger (1971) (W).
"Stellation core" describes a stellated regular (Platonic), semi-regular (Archimedean), or dual to a semi-regular (Catalan) figure.

Stellations of the octahedron

Main article: Stellated octahedron

The stella octangula (or stellated octahedron), is the only stellation of the regular octahedron.[21] This stellation is made of self-dual tetrahedra, as the simplest regular polyhedral compound:[22]

Figure Stellation
Regular octahedron
Stellated octahedron
stella octangula
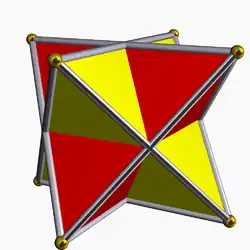Regular polytope or regular compound,
deltahedra, antiprisms

Different from the larger, regular self-dual polyhedral enantiomorphisms (such as in the compound of five cubes), the tetrahedron is the only Platonic solid to generate a stellation (and regular polyhedron compound) from a single intersecting copy of itself.[e] Like the cube, the regular tetrahedron does not generate stellations when extending its faces, since all are adjacent (this yields only one possible convex hull).[21]

Stellations of the icosahedron

Main article: The Fifty-Nine Icosahedra
Further information: List of Wenninger polyhedron models § Stellations: models W19 to W66
This is the stellation diagram of the regular icosahedron, with face sets labelled, 0-13.

Coxeter et al. (1938) details stellations of the regular icosahedron with (aformentioned) rules proposed by J. C. P. Miller. The following table lists all such stellations per the Crennells' indexing, as found in Coxeter et al. (1999). In this list,[f] the regular icosahedron (or snub octahedron) stellation core is indexed as "1" (press "show" to open the table):

Stellations of the regular icosahedron 
Crennell Cells Faces Figure Face diagram
1 A 0
2 B 1
3 C 2
4 D 3 4
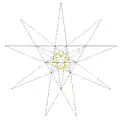5 E 5 6 7
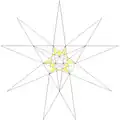6 F 8 9 10
7 G 11 12
8 H 13
9 e1 3' 5
10 f1 5' 6' 9 10
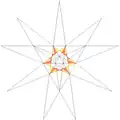11 g1 10' 12
12 e1f1 3' 6' 9 10
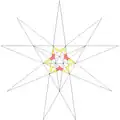13 e1f1g1 3' 6' 9 12
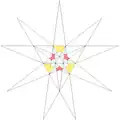14 f1g1 5' 6' 9 12
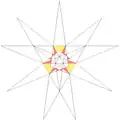15 e2 4' 6 7
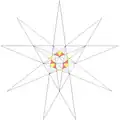16 f2 7' 8
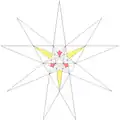17 g2 8' 9'11
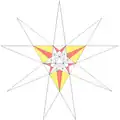18 e2f2 4' 6 8
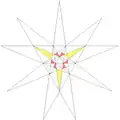19 e2f2g2 4' 6 9' 11
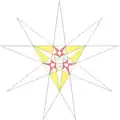20 f2g2 7' 9' 11
21 De1 4 5
22 Ef1 7 9 10
23 Fg1 8 9 12
24 De1f1 4 6' 9 10
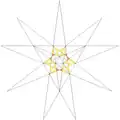25 De1f1g1 4 6' 9 12
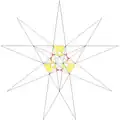26 Ef1g1 7 9 12
27 De2 3 6 7
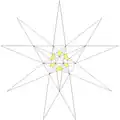28 Ef2 5 6 8
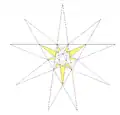29 Fg2 10 11
30 De2f2 3 6 8
31 De2f2g2 3 6 9' 11
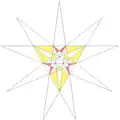32 Ef2g2 5 6 9' 11
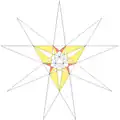33 f1 5' 6' 9 10
34 e1f1 3' 5 6' 9 10
35 De1f1 4 5 6' 9 10
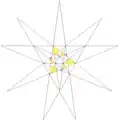36 f1g1 5' 6' 9 10' 12
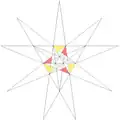37 e1f1g1 3' 5 6' 9 10' 12
38 De1f1g1 4 5 6' 9 10' 12
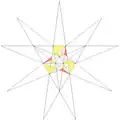39 f1g2 5' 6' 8' 9' 10 11
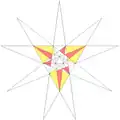40 e1f1g2 3' 5 6' 8' 9' 10 11
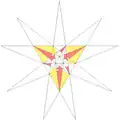41 De1f1g2 4 5 6' 8' 9' 10 11
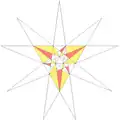42 f1f2g2 5' 6' 7' 9' 10 11
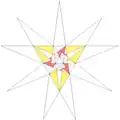43 e1f1f2g2 3' 5 6' 7' 9' 10 11
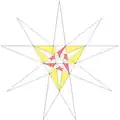44 De1f1f2g2 4 5 6' 7' 9' 10 11
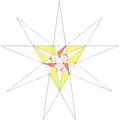45 e2f1 4' 5' 6 7 9 10
46 De2f1 3 5' 6 7 9 10
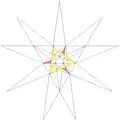47 Ef1 5 6 7 9 10
48 e2f1g1 4' 5' 6 7 9 10' 12
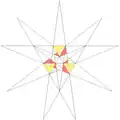49 De2f1g1 3 5' 6 7 9 10' 12
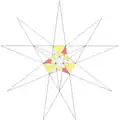50 Ef1g1 5 6 7 9 10' 12
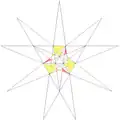51 e2f1f2 4' 5' 6 8 9 10
52 De2f1f2 3 5' 6 8 9 10
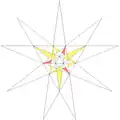53 Ef1f2 5 6 8 9 10
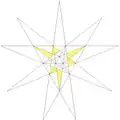54 e2f1f2g1 4' 5' 6 8 9 10' 12
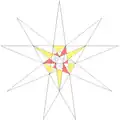55 De2f1f2g1 3 5' 6 8 9 10' 12
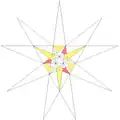56 Ef1f2g1 5 6 8 9 10' 12
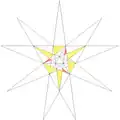57 e2f1f2g2 4' 5' 6 9' 10 11
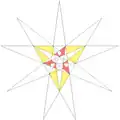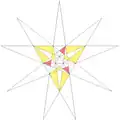
58 De2f1f2g2 3 5' 6 9' 10 11
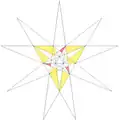
59 Ef1f2g2 5 6 9' 10 11

Wenninger (1971) includes a subset of these as formal stellations, primarily based on illustrative methods of construction of stellated polyhedral models (and extending to stellations of the icosidodecahedron).[23] While only one stellation of the icosahedron is a Kepler-Poinsot polyhedron, all stellations of the dodecahedron are Kepler-Poinsot polyhedra (the remaining).

Hemipolychrons

Further information: Hemipolyhedron § Duals of the hemipolyhedra

In Wenninger (1983), a unique family of stellations with unbounded vertices are identified.[16] These originate from orthogonal edges of faces that pass through centers of their corresponding dual hemipolyhedra. The following is a list of these stellations; specifically, of non-convex, uniform hemipolyhedra (with coincidental figures in parentheses).

Table of hemipolyhedral stellations
Image Name Stellation core
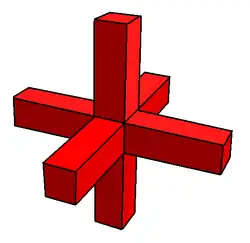  Tetrahemihexacron Tetrahemihexahedron
  Hexahemioctacron
(octahemioctacron)		 Octahemioctahedron
  Small dodecahemidodecacron   
(small icosihemidodecacron)		 Small icosihemidodecahedron
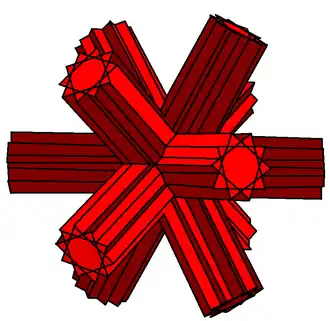  Great icosihemidodecacron
(great dodecahemidodecacron)		 Great dodecahemidodecahedron
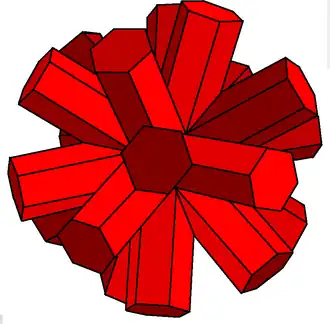  Small dodecahemicosacron
(great dodecahemicosacron)		 Great dodecahemicosahedron

This family of stellations does not strictly fulfill the definition of a polyhedron that is bound by vertices, and Wenninger notes that at the limit their facets can be interpreted as forming unbounded elongated pyramids, or equivalently, prisms (indistinguishably).[24] Of these, only the tetrahemihexahedron would produce a stellation without another coincidental figure, the tetrahemihexacron.

Notes

  1. ^ In this same work, da Vinci illustrates a concaved triakis icosahedron, which shares its outer shell with the great stellated dodecahedron.[5]
  2. ^ The core of a star polyhedron or compound is the largest convex solid that can be drawn inside them, while their case is the smallest convex solid that contains them.[15]
  3. ^ Using index notation from Coxeter et al. (1999) (C), the Crennells' third edition of The Fifty-Nine Icosahedra, and Magnus Wenninger's notation as found in Wenninger (1971) (W), where applicable.
  4. ^ Forms a honeycomb with copies of itself.[20]
  5. ^ Regular compound polyhedra larger than the stellated octahedron are made of larger sets of regular polyhedra with chiral symmetry.
  6. ^ "Cell" corresponds to the internal spaces formed by extending face-planes of the regular icosahedron (du Val notation). In a symmetric figure such as the regular icosahedron, these cell types form groups or sets of congruent cells, unique to each stellation — a set of cells forming a closed layer around its core forms a shell, which can be made of multiple types (e.g., e comprises e1 and e2).

Sources

Works cited

  1. ^ Brückner (1900), p. 260.
  2. ^ Coxeter (1969), p. 37.
  3. ^ Chasles (1875), pp. 480, 481.
  4. ^ Pacioli (1509), pls. XIX, XX.
  5. ^ Pacioli (1509), pls. XXV, XXVI.
  6. ^ Jamnitzer (1568), eng. F.IIII.
  7. ^ Jamnitzer (1568), eng. C.V.
  8. ^ Coxeter et al. (1938), pp. 7, 8.
  9. ^ a b Webb (2001), Miller's rules.
  10. ^ Messer (1995), p. 26.
  11. ^ Wenninger (1983), pp. 36, 153.
  12. ^ Messer (1995), p. 27.
  13. ^ Coxeter (1948), p. 95.
  14. ^ Coxeter (1948), p. 99.
  15. ^ Coxeter (1948), p. 98.
  16. ^ a b Wenninger (1983), pp. 101–119.
  17. ^ Pawley (1975), p. 225.
  18. ^ Weisstein.
  19. ^ Holden (1971), p. 134.
  20. ^ Holden (1971), p. 165.
  21. ^ a b Coxeter (1973), p. 96.
  22. ^ Coxeter (1973), pp. 48, 49.
  23. ^ Wenninger (1971), pp. 34–36, 41–65.
  24. ^ Wenninger (1983), pp. 101, 103, 104.

References

This article is issued from Wikipedia. The text is available under Creative Commons Attribution-Share Alike 4.0 unless otherwise noted. Additional terms may apply for the media files.