Kovasznay flow

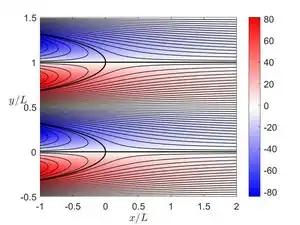
Kovasznay flow corresponds to an exact solution of the Navier–Stokes equations and are interpreted to describe the flow behind a two-dimensional grid. The flow is named after Leslie Stephen George Kovasznay, who discovered this solution in 1948.^[1] The solution is often used to validate numerical codes solving two-dimensional Navier-Stokes equations.

Let ${\displaystyle U}$ be the free stream velocity and let ${\displaystyle L}$ be the spacing between a two-dimensional grid. The velocity field ${\displaystyle (u,v,0)}$ of the Kovaszany flow, expressed in the Cartesian coordinate system is given by^[2]

${\displaystyle {\frac {u}{U}}=1-e^{\lambda x/L}\cos \left({\frac {2\pi y}{L}}\right),\quad {\frac {v}{U}}={\frac {\lambda }{2\pi }}e^{\lambda x/L}\sin \left({\frac {2\pi y}{L}}\right)}$

where ${\displaystyle \lambda }$ is the root of the equation ${\displaystyle \lambda ^{2}-Re\,\lambda -4\pi ^{2}=0}$ in which ${\displaystyle Re=UL/\nu }$ represents the Reynolds number of the flow. The root that describes the flow behind the two-dimensional grid is found to be

${\displaystyle \lambda ={\frac {1}{2}}(Re-{\sqrt {Re^{2}+16\pi ^{2}}}).}$

The corresponding vorticity field ${\displaystyle (0,0,\omega )}$ and the stream function ${\displaystyle \psi }$ are given by

${\displaystyle {\frac {\omega }{U/L}}=Re\lambda e^{\lambda x/L}\sin \left({\frac {2\pi y}{L}}\right),\quad {\frac {\psi }{LU}}={\frac {y}{L}}-{\frac {1}{2\pi }}e^{\lambda x/L}\sin \left({\frac {2\pi y}{L}}\right).}$

Similar exact solutions, extending Kovasznay's, has been noted by Lin and Tobak^[3] and C. Y. Wang.^[4][5]