Golden ellipse

A golden ellipse is an ellipse in which the aspect ratio of its two semi-axes ${\displaystyle a}$ and ${\displaystyle b}$ corresponds to the golden ratio.

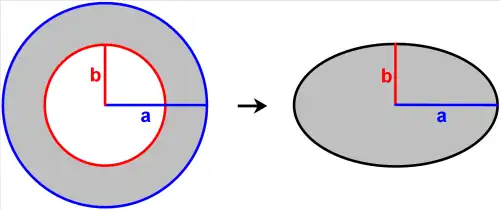
Given is a annulus with outer radius ${\displaystyle a}$ and inner radius ${\displaystyle b}$ as well as an ellipse with semi-major axis ${\displaystyle a}$ and semi-minor axis ${\displaystyle b}$, where ${\displaystyle a}$ and ${\displaystyle b}$ are positive real numbers.

Then the ratio ${\displaystyle {\frac {a}{b}}}$ corresponds to the golden ratio ${\displaystyle \Phi }$ if and only if the annulus and the ellipse have the same area. ^[1]

The proof results from the following equivalence chain:

${\displaystyle \pi a^{2}-\pi b^{2}=\pi ab\Leftrightarrow a^{2}-ba-b^{2}=0\Leftrightarrow a={\frac {b}{2}}\ \pm {\sqrt {{\frac {b^{2}}{4}}+b^{2}}}\Leftrightarrow a={\frac {1}{2}}(1\pm {\sqrt {5}})\cdot b}$

Since only the positive solution is possible, after division by ${\displaystyle b}$ we get:

${\displaystyle {\frac {a}{b}}={\frac {1}{2}}(1+{\sqrt {5}})=\Phi }$

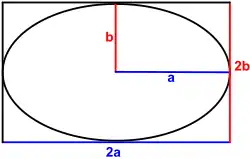
The golden ellipse can be inscribed in a golden rectangle with the side lengths ${\displaystyle 2a}$ and ${\displaystyle 2b}$.^[2]

• Anthony David Rawlins: A note on the golden ratio. Mathematical Gazette, 79, (1995), page 104

• Daniel Favre: Golden ratio (Sectio Aurea) in the Elliptical Honeycomb ResearchGate, January 2016
• Tadeusz E. Dorozinski: Goldene Ellipse on 3doro.de